不同的二叉搜索树 | LeetCode-96 | 动态规划
1.题目描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
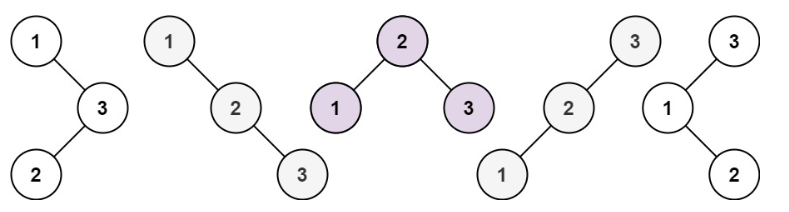
1 | 输入:n = 3 |
示例 2:
1 | 输入:n = 1 |
提示:
1 <= n <= 19
2.题解
2.1 动态规划
1 | class Solution { |
2.2 数学
卡塔兰数:
$C_0=1,\quad C_{n+1}=\frac{2(2n+1)}{n+2}C_n$
1 | class Solution { |
-------------本文结束感谢您的阅读-------------