子集 | LeetCode-78 | 回溯算法

发表于 更新于 分类于 ， ， 阅读次数： 阅读次数： Waline： 本文字数： 6.5k 阅读时长 ≈ 11 分钟
回溯算法练习题 | 子集问题
LeetCode链接：78. 子集

题目1：46. 全排列

1.题目描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

1
2
输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

1
2
输入：nums = [1]
输出：[[1]]

提示：

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums 中的所有整数 互不相同

2.题解

  • 图解：

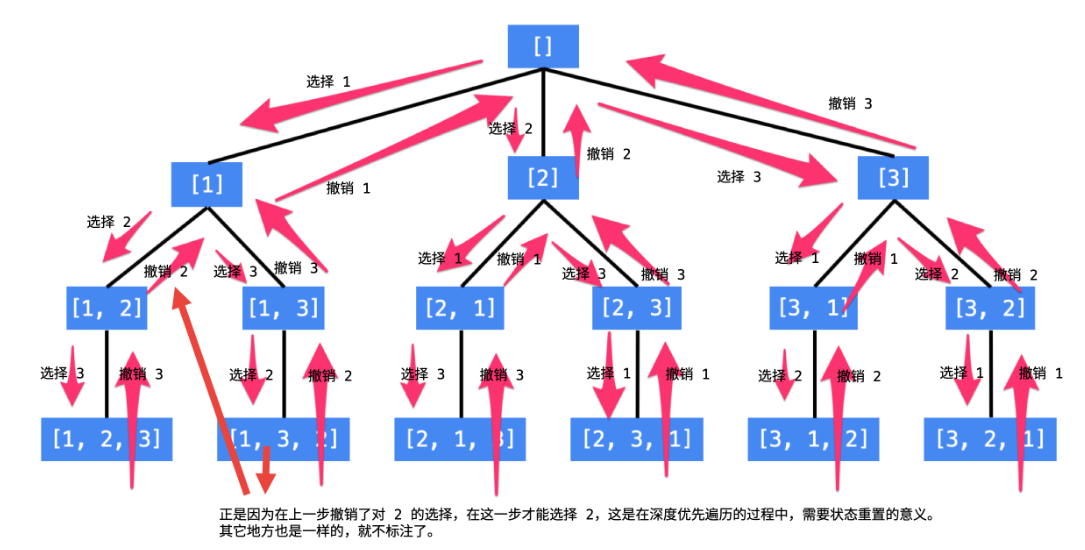
image-20240909193332821

2.1 回溯解法1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    // 定义存储最终结果的列表，result 用于存储所有可能的全排列
    List<List<Integer>> result = new ArrayList<>();
    // 定义存储当前排列路径的列表，path 用于构建当前的排列
    List<Integer> path = new ArrayList<>();

    // 主方法 permute，输入一个整数数组 nums，返回其所有全排列
    public List<List<Integer>> permute(int[] nums) {
        // 调用回溯算法，初始化一个长度为 nums.length 的布尔数组 used，用于记录每个元素是否被使用
        backtracking(nums, new boolean[nums.length]);
        // 返回最终的排列结果
        return result;
    }
    
    // 回溯算法方法 backtracking，用于生成所有可能的全排列
    public void backtracking(int[] nums, boolean[] used) {
        // 如果当前路径的长度等于数组的长度，则表示已经生成了一个完整的排列
        if (path.size() == nums.length) { 
            // 将当前路径 path 的副本加入结果列表中
            result.add(new ArrayList<>(path)); 
            return; // 结束当前递归
        } 
        
        // 遍历数组中的每一个元素
        for (int i = 0; i < nums.length; i++) {
            // 如果当前元素已经被使用，则跳过该元素
            if (used[i]) continue;
            // 标记当前元素为已使用
            used[i] = true; 
            // 将当前元素添加到排列路径 path 中
            path.add(nums[i]); 
            // 递归调用回溯函数，处理下一个元素
            backtracking(nums, used);
            // 回溯：移除路径中的最后一个元素
            path.remove(path.size() - 1); 
            // 重置当前元素的使用状态，以便下一次使用
            used[i] = false; 
        }
    }
}

2.2 回溯解法2

  • 这种写法得益于数组中没有重复元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
    // 定义存储最终结果的列表，result 用于存储所有可能的全排列
    List<List<Integer>> result = new ArrayList<>();
    // 定义存储当前排列路径的列表，path 用于构建当前的排列
    List<Integer> path = new ArrayList<>();

    // 主方法 permute，输入一个整数数组 nums，返回其所有全排列
    public List<List<Integer>> permute(int[] nums) {
        // 调用回溯算法，开始生成全排列
        backtracking(nums, new boolean[nums.length]);
        // 返回最终的排列结果
        return result;
    }

    // 回溯算法方法 backtracking，用于生成所有可能的全排列
    public void backtracking(int[] nums, boolean[] used) {
        // 如果当前路径的长度等于数组的长度，则表示已经生成了一个完整的排列
        if (path.size() == nums.length) {
            // 将当前路径 path 的副本加入结果列表中
            result.add(new ArrayList<>(path));
            return; // 结束当前递归
        }

        // 遍历数组中的每一个元素
        for (int i = 0; i < nums.length; i++) {
            // 如果 path 已经包含当前元素 nums[i]，则跳过该元素
            if (path.contains(nums[i])) continue;
            // 将当前元素添加到排列路径 path 中
            path.add(nums[i]);
            // 递归调用回溯函数，处理下一个元素
            backtracking(nums, used);
            // 回溯：移除路径中的最后一个元素
            path.remove(path.size() - 1);
        }
    }
}

题目2：47. 全排列 II

1.题目描述

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

1
2
3
4
5
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

2.题解

2.1 回溯算法-哈希集合去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    // 存储最终结果的列表，result 用于存储所有可能的全排列
    List<List<Integer>> result = new ArrayList<>();
    // 存储当前排列路径的列表，path 用于构建当前的排列
    List<Integer> path = new ArrayList<>();

    // 主方法 permuteUnique，输入一个包含重复元素的整数数组 nums，返回其所有不重复的全排列
    public List<List<Integer>> permuteUnique(int[] nums) {
        // 调用回溯算法，初始化标记数组，并开始回溯
        backtracking(nums, new boolean[nums.length]);
        // 返回最终结果
        return result;
    }

    // 回溯算法方法 backtracking，用于生成所有可能的不重复全排列
    public void backtracking(int[] nums, boolean[] used) {
        // 当路径的长度等于数组的长度时，表示已经生成一个完整的排列
        if (path.size() == nums.length) {
            // 将当前路径 path 的副本加入结果列表中
            result.add(new ArrayList<>(path));
            return; // 结束当前递归
        }

        // 使用一个 Set 集合去重，避免在同一层中使用相同的元素
        Set<Integer> set = new HashSet<>();
        // 遍历数组中的每一个元素
        for (int i = 0; i < nums.length; i++) {
            // 如果当前元素已经被使用，或在同一层中已添加到 set 集合，则跳过该元素
            if (used[i] || set.contains(nums[i])) continue;
            // 添加当前元素到 set 集合，表示在当前层已经处理过该元素
            set.add(nums[i]);
            // 标记当前元素为已使用
            used[i] = true;
            // 将当前元素添加到排列路径中
            path.add(nums[i]);
            // 递归处理下一个元素
            backtracking(nums, used);
            // 回溯：移除路径中的最后一个元素
            path.remove(path.size() - 1);
            // 重置当前元素的使用状态，以便回溯到上一步
            used[i] = false;
        }
    }
}

2.2 回溯算法-哈希数组去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    List<List<Integer>> result = new ArrayList<>(); // 存储最终结果的列表，保存所有不重复的全排列
    List<Integer> path = new ArrayList<>(); // 存储当前排列路径的列表，用于构建每一个排列

    // 主函数，输入一个包含重复数字的数组 nums，返回所有不重复的全排列
    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length]; // 标记数组，记录每个数字是否已经在当前排列中使用过
        backtracking(nums, used); // 调用回溯算法开始生成全排列
        return result; // 返回生成的所有不重复全排列结果
    }

    // 回溯算法方法，用于生成所有不重复的全排列
    public void backtracking(int[] nums, boolean[] used) {
        // 当当前排列路径的长度等于数组的长度时，表示已生成一个完整的排列
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path)); // 将当前路径保存到结果列表中
            return; // 结束当前递归
        }
        
        int[] hash = new int[21]; // 哈希数组，避免同一层中使用相同的数字，范围 [-10, 10] 映射为 [0, 20]

        // 遍历数组中的每一个元素，尝试将其加入当前排列路径
        for (int i = 0; i < nums.length; i++) {
            // 如果当前元素已经使用过，或者在本轮递归中已经处理过相同的元素，则跳过
            if (used[i] || hash[nums[i] + 10] == 1) continue;
            
            used[i] = true; // 标记该元素为已使用
            hash[nums[i] + 10] = 1; // 在哈希数组中记录该元素本轮递归已使用
            path.add(nums[i]); // 将当前元素加入排列路径
            
            backtracking(nums, used); // 递归处理下一个元素
            
            // 回溯过程：移除路径中的最后一个元素，并重置其使用状态
            path.remove(path.size() - 1); 
            used[i] = false; 
        }
    }
}

2.3 回溯算法-排序去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution {
    // 存储最终结果的列表，用于保存所有不重复的全排列
    List<List<Integer>> result = new ArrayList<>();
    // 存储当前排列路径的列表，用于构建每一个排列
    List<Integer> path = new ArrayList<>();

    // 主方法 permuteUnique，输入一个包含重复元素的整数数组 nums，返回其所有不重复的全排列
    public List<List<Integer>> permuteUnique(int[] nums) {
        // 对数组进行排序，便于后续剪枝去重
        Arrays.sort(nums);
        // 调用回溯算法，初始化标记数组并开始递归生成全排列
        backtracking(nums, new boolean[nums.length]);
        // 返回生成的所有不重复的全排列
        return result;
    }

    // 回溯算法，用于生成所有不重复的全排列
    public void backtracking(int[] nums, boolean[] used) {
        // 当路径的长度等于数组的长度时，表示已生成一个完整的排列
        if (path.size() == nums.length) {
            // 将当前路径的副本加入结果列表中
            result.add(new ArrayList<>(path));
            return; // 结束当前递归
        }

        // 遍历数组中的每一个元素，尝试将其加入当前排列路径
        for (int i = 0; i < nums.length; i++) {
            // 剪枝：跳过重复的数字
            // nums[i] == nums[i-1] 保证当前数字和前一个相同
            // used[i-1] == false 保证是在同一层级使用过该元素
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) continue;

            // 如果当前元素未使用过
            if (used[i] == false) {
                used[i] = true; // 标记当前元素为已使用
                path.add(nums[i]); // 将元素加入当前排列路径
                backtracking(nums, used); // 递归处理下一个元素
                path.remove(path.size() - 1); // 回溯，移除最后加入的元素
                used[i] = false; // 重置使用状态，以便后续递归使用
            }
        }
    }
}
  • 补充：去重最为关键的代码为：、
1
2
3
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}
  • **如果改成 used[i - 1] == true， 也是正确的!**，去重代码如下：
1
2
3
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
    continue;
}

这是为什么呢，就是上面我刚说的，如果要对树层中前一位去重，就用used[i - 1] == false，如果要对树枝前一位去重用used[i - 1] == true。

对于排列问题，树层上去重和树枝上去重，都是可以的，但是树层上去重效率更高！

这么说是不是有点抽象？

来来来，我就用输入: [1,1,1] 来举一个例子。

树层上去重(used[i - 1] == false)，的树形结构如下：

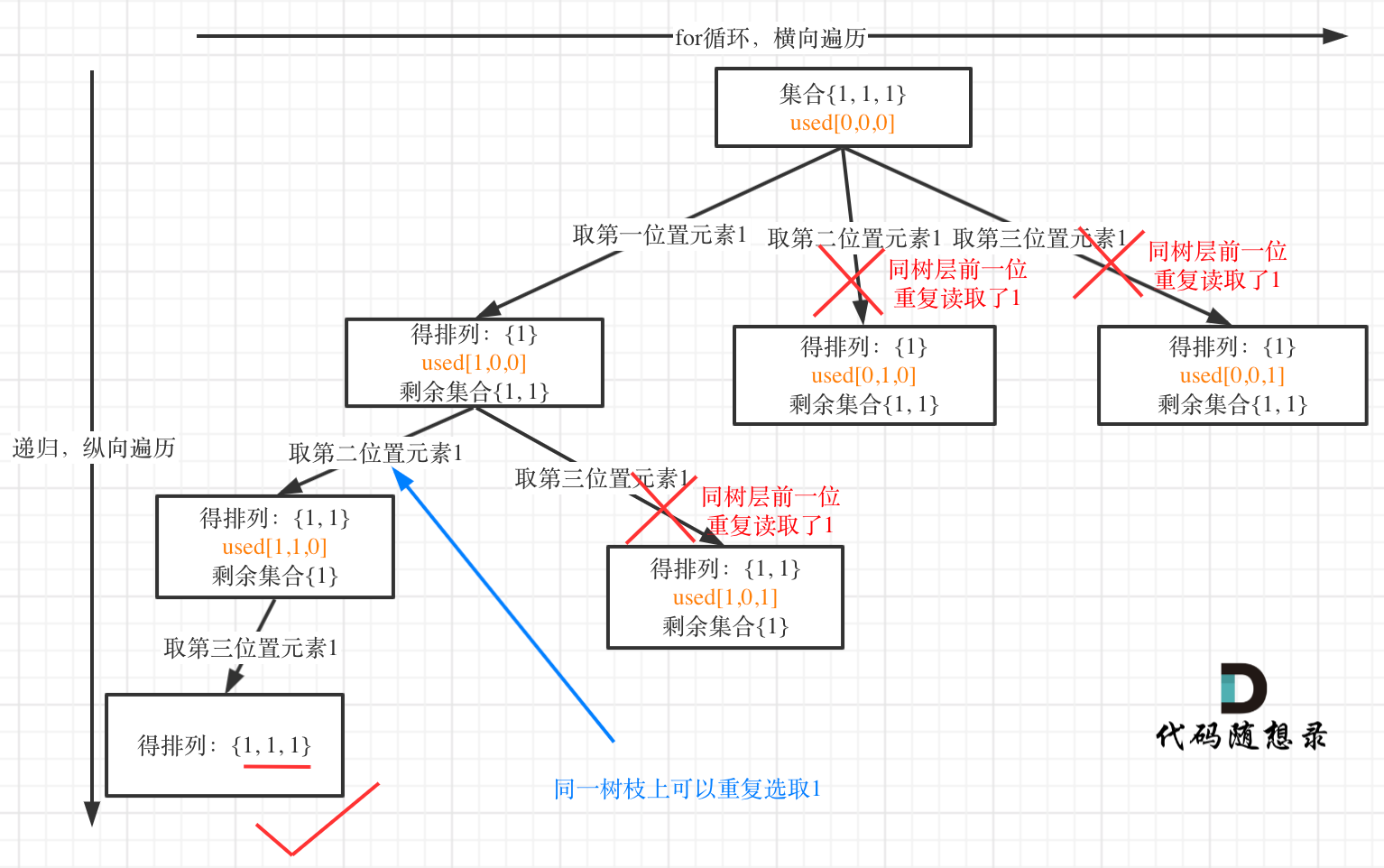
47.全排列II2

树枝上去重（used[i - 1] == true）的树型结构如下：

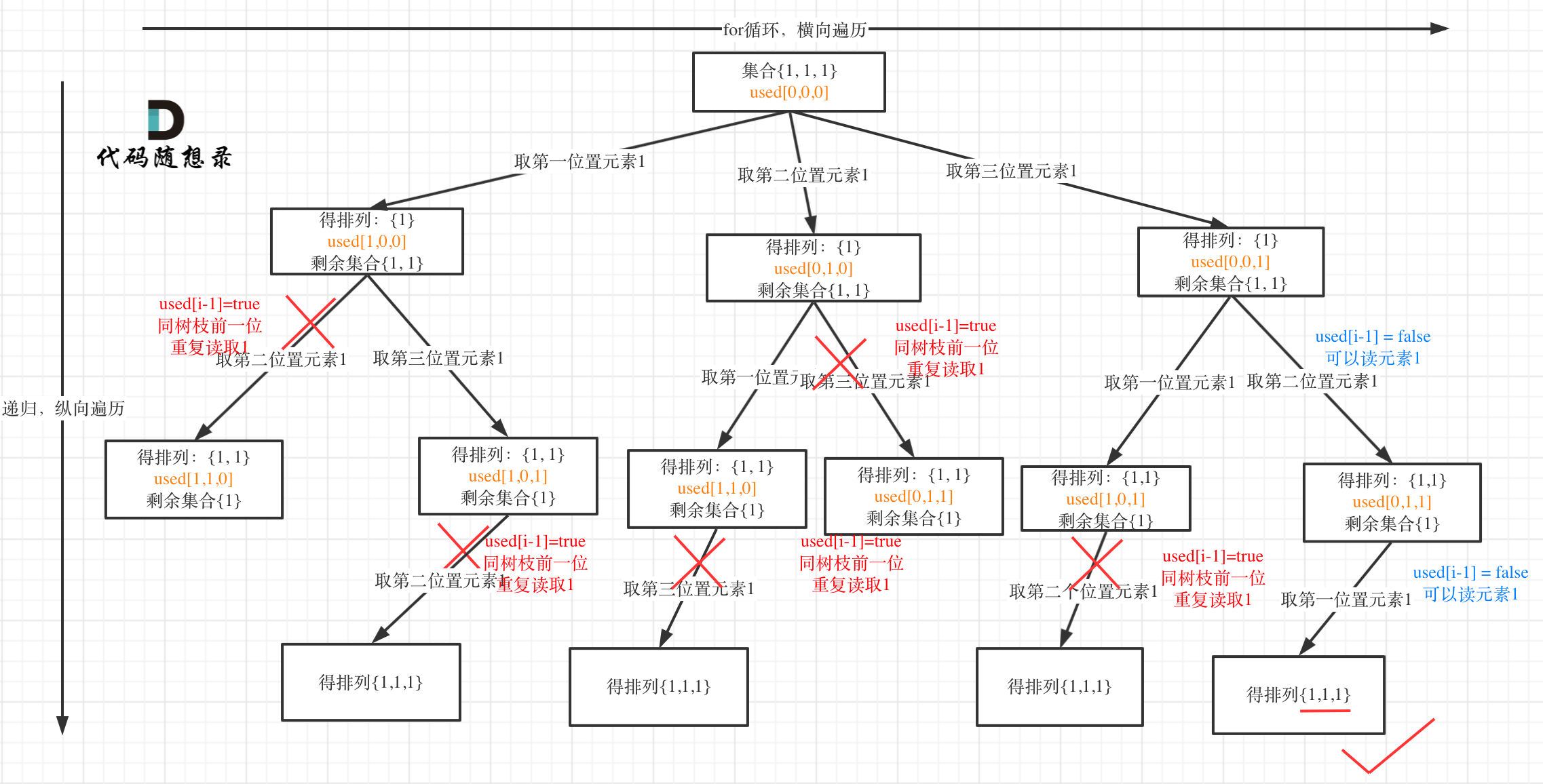
47.全排列II3

大家应该很清晰的看到，树层上对前一位去重非常彻底，效率很高，树枝上对前一位去重虽然最后可以得到答案，但是做了很多无用搜索

-------------本文结束感谢您的阅读-------------