全网超全的二分查找细节总结！ | 二分查找

发表于 2024-08-10 更新于 2025-03-10 分类于算法，算法笔记阅读次数：阅读次数： Waline：本文字数： 12k 阅读时长 ≈ 20 分钟

老子说：天下大事必作于细；天下难事必作于易，如果不知道这些细节，你就没用学明白二分查找！

1.基础版二分查找细节

今天毛毛张要分享的是LeetCode中最简单的一道题目：二分查找，二分查找算法虽然简单但却是非常难写，里面隐藏着很多细节需要注意，否则一旦变更一下要求就会出错
下面我们首先来看一下二分查找的题目：LeetCode链表：704. 二分查找
注意事项1：这道题目的前提条件是，数组中的元素按照严格升序的顺序进行排序

1.1 题目描述

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例 1:

1
2
3

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

1
2
3

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

1.2 题解

由于这个算法比较容易，毛毛张在这里不在这里详细介绍这个算法的思路，再下面介绍两种常见写法，这两种常见的写法是根据搜索区间的开闭情况来进行发分类：
- 写法模板1：搜索区间为左闭右闭$[left,right]$
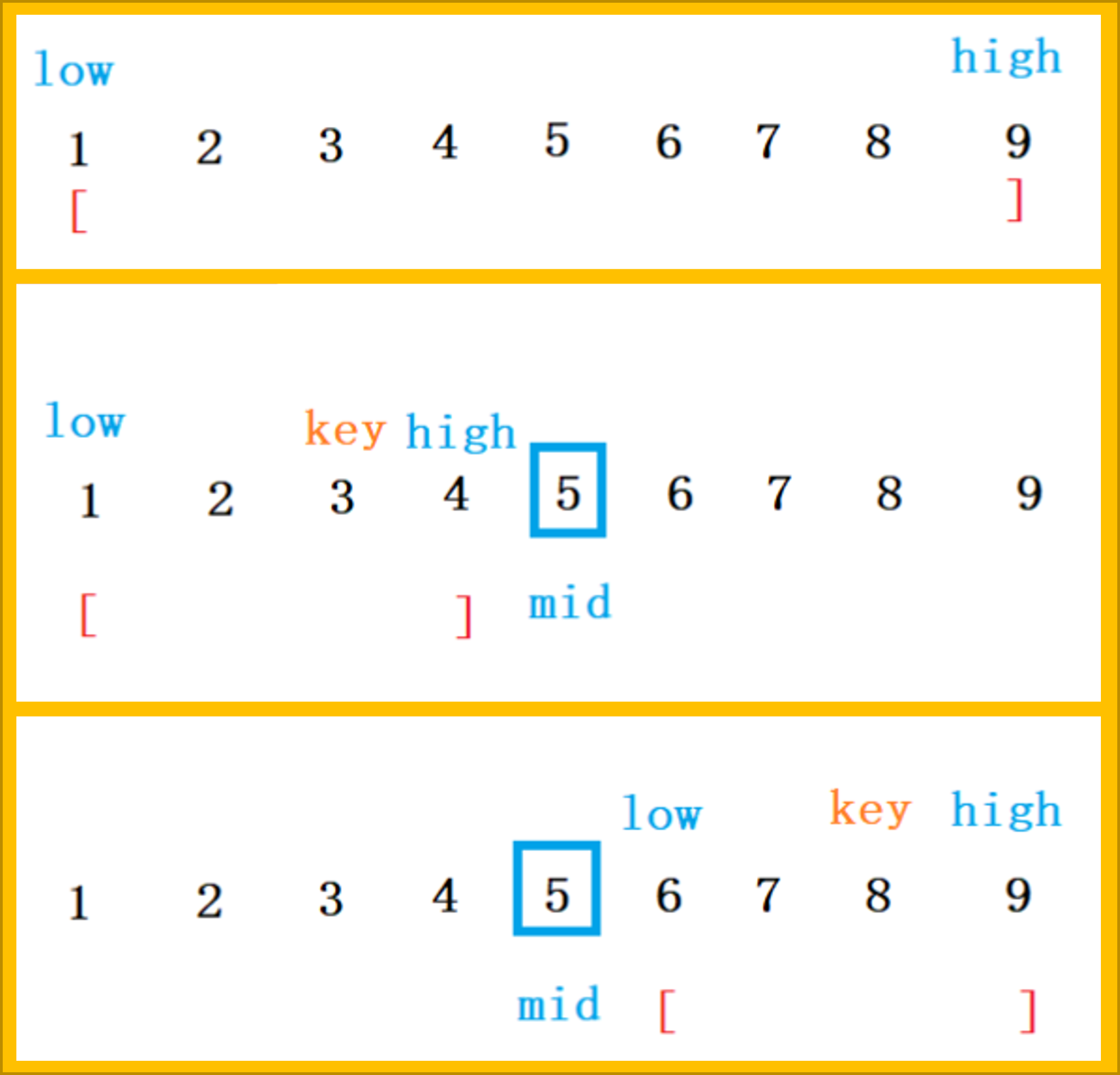
- 写法模板2：搜索区间为左闭右开$[left,right)$

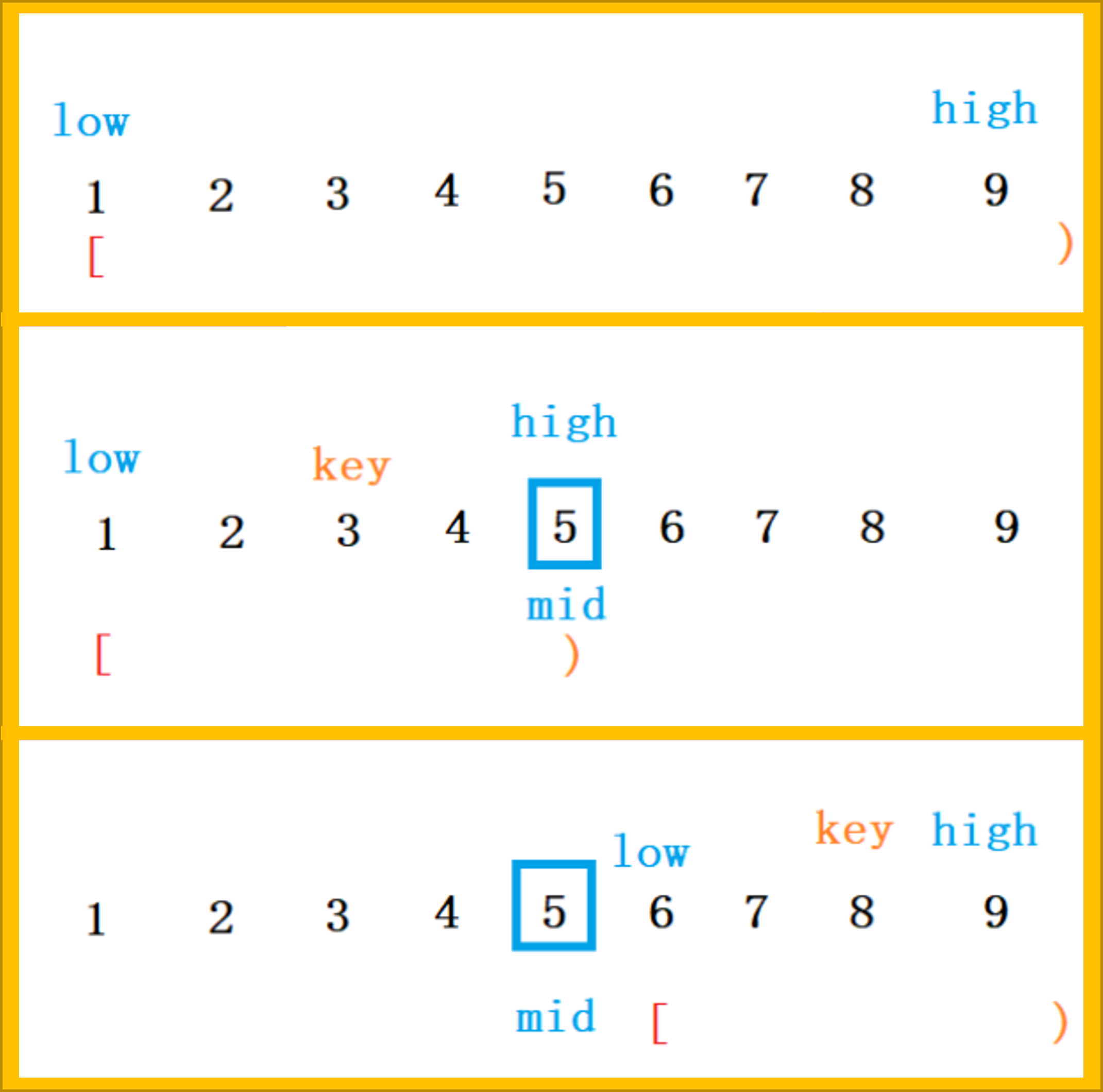
1.2.1 写法模板1

class Solution {
    public int search(int[] nums, int target) {
        // 左边索引
        int left = 0;
        // 右边索引
        int right = nums.length-1;

        // 开始二分查找逻辑
        while (left <= right) {
            // 中间索引
            int mid = (right - left) / 2 + left;
            // 获取中间值，并进行比较
            if (nums[mid] == target) {
                return mid;
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return -1;
    }
}

1.2.2 写法模板2

class Solution {
    public int search(int[] nums, int target) {
        // 左边索引
        int left = 0;
        // 右边索引
        int right = nums.length;

        // 开始二分查找逻辑
        while (left < right) {
            // 中间索引
            int mid = (right - left) / 2 + left;
            // 获取中间值，并进行比较
            if (nums[mid] == target) {
                return mid;
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        return -1;
    }
}

1.3 注意事项

1.3.1 写法转换细节

两种写法模板大体相似，但是如果两种写法在进行转换的时候需要修改三处地方，这个一定要注意，漏了一处就会出错

修改地方1：

1 2	写法模板1：int right = nums.length-1; 写法模板2：int right = nums.length;

修改地方2：

1 2	写法模板1：while (left <= right) 写法模板2：while (left < right)

修改地方3：

1 2	写法模板1：right = mid - 1; 写法模板2：right = mid;

1.3.2 取中点环节`(left + right)/2`

1. `(left + right) / 2`

这个表达式直接将 left 和 right 相加，然后除以 2。主要的问题是，如果 left 和 right 的值很大，那么 left + right 的结果可能会超过 int 类型的最大值（即 Integer.right_VALUE），导致 整数溢出。在发生溢出时，计算结果会不正确。

举例：

1
2
3

int left = Integer.right_VALUE - 1;  // 2147483646
int right = Integer.right_VALUE;     // 2147483647
int mid = (left + right) / 2;        // 溢出，结果错误

在这种情况下，left + right 会溢出为负数，导致 mid 计算出错误的结果。

2. `left + (right - left) / 2` (推荐)

这个表达式通过先计算 right - left 的差值，再除以 2，并加上 left。这种方法避免了直接相加导致的溢出问题，因为 right - left 是一个相对较小的值，left + (right - left) / 2 不会溢出。

举例：

1
2
3

int left = Integer.right_VALUE - 1; // 2147483646
int right = Integer.right_VALUE;     // 2147483647
int mid = left + (right - left) / 2; // 正确的结果，不会溢出

3.`(left+ right)>>>1`（推荐）

将 left + right 的结果右移一位（相当于除以 2），使用无符号右移操作符 >>> 来计算中间值。
避免溢出: 虽然 left + right 可能溢出，但右移操作可以处理溢出的情况，得到正确的结果。
效率高: 位运算通常比算术运算更快，因此这种方法在某些情况下性能更好。

举例：

1
2
3

int left = Integer.right_VALUE - 1;
int right = Integer.right_VALUE;
int mid = (left + right) >>> 1; // 结果为 2147483646，正确且不溢出

1.3.3 `left`与`right`

写法模板1

class Solution {
    public int search(int[] nums, int target) {
        // 左边索引
        int left = 0;
        // 右边索引
        int right = nums.length-1;

        // 开始二分查找逻辑
        while (left <= right) {
            // 中间索引
            int mid = (right - left) / 2 + left;
            // 获取中间值，并进行比较
            if (nums[mid] == target) {
                return mid;
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return -1;
    }
}

在写法模板1中有如下结论：
- 如果目标值在数组中： 正常返回索引mid，且此时的left与right不一定等于mid，没有什么关系
- 如果目标值不在数组中：
  - 结论1：退出循环时的条件为left=right+1
  - 结论2：此时的left表征的是按照升序排序要插入在数组中的索引的位置，即插入点的位置；另一种说法，此时left的索引上的元素大于目标值target（在题目开始说过了，数组中的元素按照严格升序进行排序，如果不是则不一定）

写法模板2

class Solution {
    public int search(int[] nums, int target) {
        // 左边索引
        int left = 0;
        // 右边索引
        int right = nums.length;

        // 开始二分查找逻辑
        while (left < right) {
            // 中间索引
            int mid = (right - left) / 2 + left;
            // 获取中间值，并进行比较
            if (nums[mid] == target) {
                return mid;
            } else if (target > nums[mid]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        return -1;
    }
}

注意事项2：这种写法，如果退出循环的条件写成while(left <= right)，如果目标值不存在，则会进入死循环
在写法模板2中有如下结论：
- 如果目标值在数组中： 正常返回索引mid，且此时的left与right不一定等于mid，没有什么关系
- 如果目标值不在数组中：
  - 结论1：退出循环时的条件为left=right
  - 结论2：此时的left表征的是按照升序排序要插入在数组中的索引的位置，即插入点的位置；另一种说法，此时left的索引上的元素大于目标值target（在题目开始说过了，数组中的元素按照严格升序进行排序，如果不是则不一定）

在Java底层类库源码中，正式利用了二分查找在找不到的元素的时候索引left的特征对代码进行了优化

1.4 Java源码解读

二分查找算法已经被封装在Arrays类中，该类位于java.util.Arrays中，如果需要使用，可以直接导包

import java.util.Arrays;

public class Test{
    public static void main(String[] args){
        Arrays.binarySearchint[] a, int froleftdex, int toIndex, int key);
    }
}

源码：

/*
Searches a range of the specified array of ints for the specified value using the binary search algorithm. The range must be sorted (as by the sort(int[], int, int) method) prior to making this call. If it is not sorted, the results are undefined. If the range contains multiple elements with the specified value, there is no guarantee which one will be found.

Params:a – the array to be searched 
	   froleftdex – the index of the first element (inclusive) to be searched 
	   toIndex – the index of the last element (exclusive) to be searched 
	   key – the value to be searched for
	   
Returns:index of the search key, if it is contained in the array within the specified range; otherwise, (-(insertion     point) - 1). The insertion point is defined as the point at which the key would be inserted into the array: the index of the first element in the range greater than the key, or toIndex if all elements in the range are less than the specified key. Note that this guarantees that the return value will be >= 0 if and only if the key is found.

Throws:IllegalArgumentException – if froleftdex > toIndex
       ArrayIndexOutOfBoundsException – if froleftdex < 0 or toIndex > a. length
*/
public static int binarySearch(int[] a, int froleftdex, int toIndex, int key) {
        rangeCheck(a.length, froleftdex, toIndex);
        return binarySearch0(a, froleftdex, toIndex, key);
}

// 二分查找源码
private static int binarySearch0(int[] a, int froleftdex, int toIndex, int key) {
    int low = froleftdex;
    int high = toIndex - 1;

    while (low <= high) {
        int mid = (low + high) >>> 1;
        int midVal = a[mid];

        if (midVal < key)
            low = mid + 1;
        else if (midVal > key)
            high = mid - 1;
        else
            return mid; // key found
    }
    return -(low + 1);  // key not found.
}

源码解读：
- Java中的二分查找的源码为使用的是写法模板1的形势来进行查找的
- 二分查找返回值：
  - 如果能找到目标值，则返回的是目标值的索引
  - 如果找不到，返回值的是要插入位置的索引加1的相反数，例如：要插入的索引是5，则返回-6 = -(5+1)

2.进阶版二分查找细节

上面的基础班的二分查找中，数组中元素的顺序是按照严格升序排序的顺序，也就是说没用重复元素，而下面介绍的进阶版就是，数组中存在相同的元素。
LeetCode链接：34. 在排序数组中查找元素的第一个和最后一个位置

2.1 题目描述

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1 2	输入：nums = [5,7,7,8,8,8,10], target = 8 输出：[3,5]

示例 2：

1 2	输入：nums = [5,7,7,8,8,10], target = 6 输出：[-1,-1]

示例 3：

1 2	输入：nums = [], target = 0 输出：[-1,-1]

提示：

$0 <= nums.length <= 10^5$
$-10^9 <= nums[i] <= 10^9$
nums 是一个非递减数组
$-10^9 <= target <= 10^9$

2.2 题解

基础版的二分查找，只能返回找到目标值时的索引，无法找到目标值存在多个时的开始索引和结束索引
下面毛毛张将来介绍一下如何改动基础的二分查找实现找到目标值的开始索引和结束索引，以写法模板1为例
我们只需要新设置一个变量，用来表征返回索引的候选值即可，不断更新这个索引，先以找开始索引为例

2.2.1 找开始索引

public int Leftmost(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    int candidate = -1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            candidate = mid;
            right = mid - 1;
        }else if (nums[mid] > target) {
            right = mid - 1;
        }else {
            left = mid + 1;
        }
    }
    return candidate;
}

由于target == nums[mid]和target < nums[mid] 这两种情况下收缩区间的方式是一样的，因此我们可以优化一下代码

public int Leftmost(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target <= nums[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return nums[left] == target ? left : -1;
}

索引left含义：在前面说过，这种情况下退出循环的条件是left = right+1，所以就没必要说right的含义了
- 如果目标值存在，left就是目标值的最左边的索引，也就是开始索引。
- 如果目标值不存在，就是目标值要插入的位置的索引；另一种说法，left索引大于目标值的最靠左的元素的索引
- 综上所述，上面代码中索引left的含义是：大于等于target的最靠左的元素的索引
索引right：无论目标值是否存在，right表征的是小于目标值最靠右的元素的索引

2.2.2 找结束索引

现在来说找结束索引

public int Rightmost(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    int candidate = -1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target == nums[mid]) {
            candidate = mid;
            left = mid + 1;
        } else if(target > nums[mid]){
            left = mid + 1;
        }else{
            right = mid - 1;
        }
    }
    return candidate;
}

由于target == nums[mid]和target > nums[mid] 这两种情况下收缩区间的方式是一样的，因此我们可以优化一下代码

public int Rightmost(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return target == nums[left - 1] ? left - 1 : -1;
}

索引left-1=right含义：在前面说过，这种情况下退出循环的条件是left = right+1，所以就没必要说right的含义了
- 如果目标值存在，left-1就是目标值的元素最左边的索引，也就是开始索引
- left-1索引表征的是小于目标值的最靠右的元素的索引
- 综上所述，上面代码中索引left-1的含义是：小于等于target的最靠右的元素的索引

2.2.3 题解

public class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] result = new int[2];
        result[0] = Leftmost(nums, target);
        result[1] = Rightmost(nums, target);
        return result;
    }

    // 查找目标值的最左边界
    private int Leftmost(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (target <= nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        // 使用 left 进行判断
        if (left < nums.length && nums[left] == target) {
            return left;
        }
        return -1;
    }

    // 查找目标值的最右边界
    private int Rightmost(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (target < nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        // 使用 right 进行判断
        if ((left -1) >= 0 && nums[(left -1)] == target) {
            return (left -1);
        }
        return -1;
    }
}

3.再探进阶版二分查找细节

在进阶版二分查找细节中，毛毛张使用的是写法模板1，但是写法模板2的的含义是否是一样的呢？
- 毛毛张在这里告诉你肯定的答案：用写法模板2，索引left和left-1的含义和写法模板1中的对应的返回值的含义是一摸一样的
在上面一题中二分查找的写法是适配题目的，在返回的时候增加了一些判断，下面毛毛张介绍一下纯净版的进阶二分查找代码模板

3.1 纯净版进阶二分查找写法

3.1.1 写法模板1

1.找开始索引

结论1：返回值left为大于等于目标值的最靠左的元素的索引（此时left = right + 1）
- 如果目标值存在，返回值left就是等于目标值的最靠左的索引
- 如果目标值不存在，返回值left就是大于目标值的最靠左的元素的索引
结论2： right无论目标值是否存在，都表征的是小于目标值最靠右的元素的索引（不要硬记，记住第一个结论，会推出这个结论）

代码：

public int Leftmost(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target <= nums[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

2.找结束索引

结论1：返回值left-1=right为小于等于目标值的最靠右的元素的索引
- 如果目标值存在，返回值left-1就是等于目标值的最靠右的索引
- 如果目标值不存在，返回值left-1就是小于目标值的最靠右的元素的索引

代码：

public static int Rightmost(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid]) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return left - 1;
}

3.1.2 写法模板2

如果用写法模板2来写进阶版二分查找，返回值的结论一模一样

1.找开始索引

结论1：返回值left为大于等于目标值的最靠左的元素的索引（此时left = right）
- 如果目标值存在，返回值left就是等于目标值的最靠左的索引
- 如果目标值不存在，返回值left就是大于目标值的最靠左的元素的索引

代码：

public int Leftmost(int[] nums, int target) {
    int left = 0, right = nums.length;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (target <= nums[mid]) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

2.找结束索引

结论1：返回值left-1为小于等于目标值的最靠右的元素的索引（此时left = right）
- 如果目标值存在，返回值left-1就是等于目标值的最靠右的索引
- 如果目标值不存在，返回值left-1就是小于目标值的最靠右的元素的索引

代码：

public static int Rightmost(int[] nums, int target) {
    int left = 0, right = nums.length;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid]) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left - 1;
}

3.2 应用

我们把找开始开始索引的函数用Leftmost函数表示，找结束索引的函数用法Rightmost函数表示，根据上面我们可以得到如下结论：

上面两个函数的应用，我们可以结合下面这个图来理解：

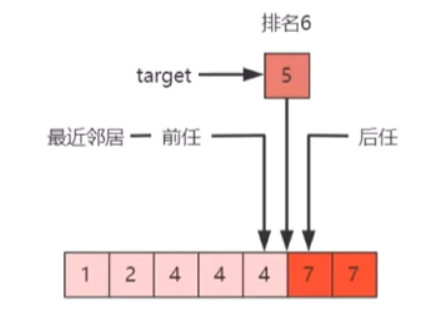
作用1：求排名，求在非递减顺序排列的整数数组，目标元素在数组中的排名
- 举例：目标值是5，排名计算公式：Leftmost(5)+1 = 5 + 1（数组中索引是0从开始的，排名是从1开始的）
作用2：求前任的索引
- 举例：目标值是5，求5的前任，计算公式：Leftmost(5) - 1 (求索引是从0开始的)
作用3：求后任的索引
- 举例：目标值时5，求5的后任，计算公式：Rightmost(5) + 1
作用4：求区间
- 举例1：小于4的区间索引区间表示：[0,Leftmost(4) - 1]
- 举例2：小于等于4的区间索引区间表示：[0,Leftmost(4)]
- 举例3：大于4的区间索引区间表示：[Rightmost(4)+1,无穷大]
- 举例4：大于等于4的区间索引区间表示：[Leftmost(4),无穷大]
- 举例5：大于等于4，小于等于7的区间索引：[Leftmost(4),Rightmost(7)]
- 举例6：大于4，小于7的区间索引：[Rightmost(4)+1,Leftmost(7)-1]

3.3 优化

上面的找开始索引和结束索引的地方存在大量的代码相似的地方，只在target < num[mid]和target <= num[mid]存在区别，于是我们可以增设一个标志位来对代码进行优化，使得代码更加简洁

3.3.1 写法模板1优化

public int binaySearch(int[] nums, int target, boolean flag) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid] || (flag && target <= nums[mid])) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return flag == true ? left : left - 1;
}

3.3.2 写法模板2优化

public int binaySearch(int[] nums, int target, boolean flag) {
    int left = 0, right = nums.length;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid] || (flag && target <= nums[mid])) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return flag == true ? left : left - 1;
}

4.练习题

参考文献

-------------本文结束感谢您的阅读-------------

1.基础版二分查找细节

1.1 题目描述

1.2 题解

1.2.1 写法模板1

1.2.2 写法模板2

1.3 注意事项

1.3.1 写法转换细节

1.3.2 取中点环节(left + right)/2

1. (left + right) / 2

2. left + (right - left) / 2 (推荐)

3.(left+ right)>>>1（推荐）

1.3.3 left与right

写法模板1

写法模板2

1.4 Java源码解读

2.进阶版二分查找细节

2.1 题目描述

2.2 题解

2.2.1 找开始索引

2.2.2 找结束索引

2.2.3 题解

3.再探进阶版二分查找细节

3.1 纯净版进阶二分查找写法

3.1.1 写法模板1

1.找开始索引

2.找结束索引

3.1.2 写法模板2

1.找开始索引

2.找结束索引

3.2 应用

3.3 优化

3.3.1 写法模板1优化

3.3.2 写法模板2优化

4.练习题

参考文献

1.3.2 取中点环节`(left + right)/2`

1. `(left + right) / 2`

2. `left + (right - left) / 2` (推荐)

3.`(left+ right)>>>1`（推荐）

1.3.3 `left`与`right`