二叉树前序遍历、中序遍历、后序遍历和层序遍历 | 递归法 | 迭代法 | 统一迭代法 | 深度优先搜索 | 广度优先搜索

今天毛毛张要分享的内容是LeetCode的刷题笔记，主要介绍的二叉树前序遍历、中序遍历、后序遍历和层序遍历思想和多种代码实现，二叉树的遍历对于二叉树后面的题目的实现具有很重要的意义

1.概述

• LeetCode题目链接：

  • Problem: 144. 二叉树的前序遍历
  • Problem: 94.二叉树的中序遍历
  • Problem: 145.二叉树的后序遍历
  • Problem: 102. 二叉树的层序遍历
  • Problem: 107. 二叉树的层序遍历 II

• 二叉树的遍历方式有多种，毛毛张今天在这里结合代码随想录的教程来分享一下二叉树的多种遍历方式及代码实现

• 二叉树主要有两种遍历方式：深度优先遍历和广度优先遍历

• 深度优先遍历： 树是图的一种特例(连通无环的图就是树)，主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成，它的特点是不撞南墙不回头，先走完一条路，再换一条路继续走

  • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）

• 广度优先遍历：一层一层的去遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点

  • 层次遍历（递归法，迭代法）

• 在深度优先遍历中：有三个顺序，前中后序遍历。这里前中后，其实指的就是中间节点的遍历顺序，只要大家记住 前中后序指的就是中间节点的位置就可以了。看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式：

  • 前序遍历：中左右
  • 中序遍历：左中右
  • 后序遍历：左右中

• 大家可以对着如下图，看看自己理解的前后中序有没有问题：

  

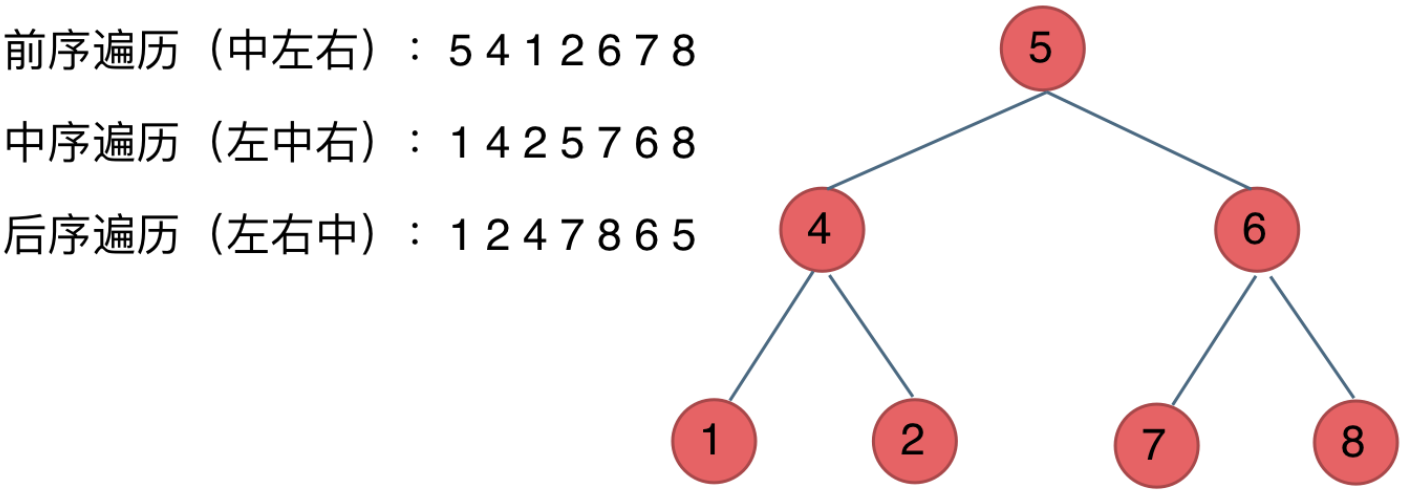
• 在做二叉树的相关题目的时候，在使用深度优先遍历的时候一般会使用递归方法来实现

• 而栈其实就是一种递归的一种实现结构，前中后序遍历的逻辑其实都是可以借助栈使用递归的方式来实现的，由此衍生出一种迭代法

• 而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

• 下面开始逐一介绍各种方法的代码实现，虽然方法名被概括为精炼的几个字，但是在具体的代码实现的时候，可能根据书写习惯的不同又会分成不同的实现方法，所以毛毛张在这里介绍几种常见的书写方法。

2.深度优先遍历：递归实现

深度优先遍历的递归实现比较简单，毛毛张在这里不做过多的赘述，只介绍一下代码随想录中的递归方法论，记住这个方法论有助于在解题的过程中不会漏掉特殊情况或者某一步骤。

• 递归的方法论：
  1. 确定递归函数的参数和返回值： 确定哪些参数是递归的过程中需要处理的，那么就在递归函数里加上这个参数， 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
  2. 确定终止条件： 写完了递归算法, 运行的时候，经常会遇到栈溢出的错误，就是没写终止条件或者终止条件写的不对，操作系统也是用一个栈的结构来保存每一层递归的信息，如果递归没有终止，操作系统的内存栈必然就会溢出。
  3. 确定单层递归的逻辑： 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。

2.1 前序遍历（递归法）

方法1：新建递归函数

实现思路： 在力扣的模板中会默认给你提供一个前序遍历的函数体，该方法在书写的时候没有使用默认的函数体作为递归函数，因为这个函数已经给你规定好了递归函数的形参和返回值，不利于理解，毛毛张在这里是单独新建一个递归函数供其调用，这种方式更加容易理解。

Code：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //1.创建List用来存放返回值
        List list = new ArrayList<Integer>();

        //2.开始前序遍历
        preOrder(root,list);

        //3.返回结果
        return list;
    }

    //递归的实现方式
    //方法论：
    //1.首先确定递归函数的形参和返回值
    public void preOrder(TreeNode node,List list){
        //2.确定终止条件
        if(node == null){
            return;
        }

        //3.确定单层递归的逻辑
        list.add(node.val);
        preOrder(node.left,list);
        preOrder(node.right,list);

    }

}

方法2：使用默认递归函数

为了完整性，毛毛张当然也要在这里给出使用提供的默认函数作为递归函数的代码啦！

Code：

class Solution {
    //递归的实现方式
    //方法论：
    //1.首先确定递归函数的形参和返回值
    //这里直接使用题目帮你确定的形参和返回值
    public List<Integer> preorderTraversal(TreeNode root) {
        //创建List用来存放返回值
        List<Integer> list = new ArrayList<>();
        
        //2.确定终止条件
        if(root == null){
            return list;
        }

        //3.确定单层递归的逻辑
        //中
        list.add(root.val);
        //左子树
        List<Integer> leftList = preorderTraversal(root.left);
        list.addAll(leftList);
        //右子树
        List<Integer>  rightList = preorderTraversal(root.right);
        list.addAll(rightList);

        return list;
    }
}

错解：

方法2这里直接使用题目帮你确定的形参和返回值

同时在确定终止条件的时候需要注意要返回一个空列表，不要写成return null

大家可用在leetcode中实战对比一下下面这写法

错解代码：

class Solution {
    //递归的实现方式
    //方法论：
    //1.首先确定递归函数的形参和返回值
    //这里直接使用题目帮你确定的形参和返回值
    public List<Integer> preorderTraversal(TreeNode root) {
        //创建List用来存放返回值
        List<Integer> list = new ArrayList<>();

        //2.确定终止条件
        if(root == null){
            return null;
        }

        //3.确定单层递归的逻辑
        //中
        list.add(root.val);
        //左子树
        List<Integer> leftList = preorderTraversal(root.left);
        list.addAll(leftList);
        //右子树
        List<Integer>  rightList = preorderTraversal(root.right);
        list.addAll(rightList);

        return list;
    }
}

2.2 中序遍历（递归法）

方法1：新建递归函数

实现思路： 在立扣的模板中会默认给你提供一个中序遍历的函数体，该方法在书写的时候没有使用默认的函数体作为递归函数，因为这个函数已经给你规定好了递归函数的形参和返回值，不利于理解，毛毛张在这里是单独新建一个递归函数供其调用，这种方式更加容易理解。

Code：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        //1.创建列表存储返回值
        List<Integer> list = new ArrayList<>();

        //2.开始中序遍历
        inOrder(root,list);

        //3.返回结果
        return list;
    }

    //递归方法论：
    //1.确定递归函数的形参和返回值
    public void inOrder(TreeNode node,List<Integer> list){
        //2.确定终止条件
        if(node == null){
            return;
        }

        //3.确定单层递归逻辑
        inOrder(node.left,list);
        list.add(node.val);
        inOrder(node.right,list);
    }
}

方法2：使用默认递归函数

Code：

class Solution {
    //递归方法论
    //1.直接使用题目帮你确定好的形参和返回值
    public List<Integer> inorderTraversal(TreeNode root) {
        //创建返回值
        List<Integer> list = new ArrayList<>();

        //2.确定终止条件
        if(root == null){
            return list;
        }

        //3.确定单层递归逻辑
        //左子树
        List<Integer> leftList = inorderTraversal(root.left);
        list.addAll(leftList);
        //中
        list.add(root.val);
        //右子树
        List<Integer> rightList = inorderTraversal(root.right);
        list.addAll(rightList);

        //返回结果
        return list;
    }
}

2.3 后序遍历（递归法）

方法1：新建递归函数

Code：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        //1.创建列表存储返回值
        List<Integer> list = new ArrayList<>();

        //2.开始后序遍历
        postOrder(root,list);

        //3.返回结果
        return list;
    }

    //递归方法论：
    //1.确定递归函数的形参和返回值
    public void postOrder(TreeNode node,List<Integer> list){
        //2.确定终止条件
        if(node == null){
            return;
        }

        //3.确定单层递归逻辑
        postOrder(node.left,list);
        postOrder(node.right,list);
        list.add(node.val);
    }
}

方法2：使用默认递归函数

Code：

class Solution {
    //后序遍历
    //递归方法
    //方法论
    //1.这里直接使用题目帮你确定好的形参和返回值
    public List<Integer> postorderTraversal(TreeNode root) {
        
        //创建列表存储返回值
        List<Integer> list = new ArrayList<>();

        //2.确定终止条件
        if(root == null){
            return list;
        }

        //3.确定单层递归逻辑
        //左子树
        List<Integer> leftList = postorderTraversal(root.left);
        list.addAll(leftList);

        //右子树
        List<Integer> rightList = postorderTraversal(root.right);
        list.addAll(rightList);

        //中间
        list.add(root.val);

        //返回结果
        return list;
    }
}

3.深度优先遍历：迭代法

• 迭代法的实现需要借助栈，下面首先介绍以下三种遍历的迭代法的算法原理，在分析原理的时候，均以下图为例：

  

3.1 原理分析

3.1.1 前序遍历与中序遍历

• 前序遍历和中序遍历的基本思想是类似的，只需把访问结点操作放在入栈操作的前面，但是前序遍历的逻辑不是很好叙述，大家可以看完中序遍历的逻辑，在结合中序遍历和前序遍历的代码来体会前序遍历的这句话

• 分析：中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了和前序遍历的处理顺序和访问顺序是不一致的

• 中序遍历的访问过程：

  • 第1步：沿着根的左孩子，依次入栈，直到左孩子为空，说明已找到可以输出的结点，此时栈内元素依次为ABD；

  • 第2步：栈顶元素出栈并访问：若其右孩子为空，继续执行第2步；若其右孩子不空，将右子树转执行第1步。

• 整个过程：

  • 栈顶D出栈并访问，它是中序序列的第一个结点，
  • D右孩子为空，栈顶B出栈并访问；（第2步）
  • B右孩子不空，将其右孩子E入栈；（第1步）
  • E左孩子为空，栈顶E出栈并访问；（第2步）
  • E右孩子为空，栈顶A出栈并访问；（第2步）
  • A右孩子不空，将其右孩子C入栈；（第1步）
  • C左孩子为空，栈顶C出栈并访问；（第2步）
  • 由此得到中序遍历结果：DBEAC

3.1.2 后序遍历

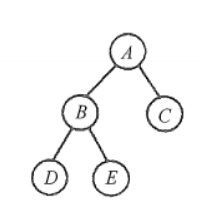
• 后序遍历的非递归实现是三种遍历方法中最难的，因为在后序遍历中，要保证左孩了和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点，这就为流程的控制带来了难题。

• 算法思想：后序非递归遍历二叉树是先访问左子树，再访问右子树，最后访问根结点

  • 第1步：沿着根的左孩子，依次入栈，直到左孩子为空，此时栈内元素依次为ABD
  • 第2步：读栈顶元素，若其右孩子不空且未被访问过，将右子树转执行第1步；否则，栈顶元素出栈并访问

• 代码实现细节：在上述思想的第2步中，必须分清返回时是从左子树返回的还是从右子树返回的，因此设定一个辅助指针r，指向最近访问过的结点。也可在结点中增加一个标志域，记录是否已被访问

• 实例过程分析：

  • 栈顶D的右孩子为空，出栈并访问，它是后序序列的第一个结点；
  • 栈顶B的右孩子不空且未被访问过，E入栈，栈顶E的左右孩子均为空，出栈并访问；
  • 栈顶B的右孩子不空但已被访问，B出栈并访问；
  • 栈项A的右孩子不空且未被访问过，C入栈，栈项C的左右孩子均为空，出栈并访问；
  • 栈顶A的右孩子不空但已被访问，A出栈并访问，由此得到后序序列DEBCA

• 我们再来分析后序遍历的第二种实现方式：要实现前面的这个逻辑还是比较复杂的，先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转结果数组，输出的结果顺序就是左右中了

  • 图解：

3.2 前序遍历（迭代法）

• 分析：前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子
  • 为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。

方法1：单层循环

单层循环和双层循环有细微的差别，大家可以自己看代码，根据自己的习惯来写

实现１：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //非递归算法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Stack<TreeNode> stack = new Stack<>();       
        TreeNode cur = root;
        //注意，第一次进入循环的结果是判断根节点root是否为空！
        while(cur != null || !stack.isEmpty()){
            //沿着根的左孩子，依次入栈
            //如果左孩子不为空，会一直执行if语句体
            if(cur != null){
                //每次访问左孩子的同时就是在访问中间结点
                //前序遍历需要把中间结果进行输出
                //因此每次判断把中间结果进行保存
                list.add(cur.val);
                stack.push(cur);
                cur = cur.left;
            }
            else{
                //直到左孩子为空，说明当前结点的左孩子已经没有了
                //就需要访问当前结点的右孩子的左孩子
                cur = stack.pop();
                cur = cur.right;
            }
        }

        //返回结果
        return list;
    }
}

实现２：

只有前序遍历能这样实现

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //迭代法 借助栈
        //创建对返回值
        List<Integer> list = new ArrayList<>();
        //判断特殊情况
        if(root == null){
            return list;
        }
        //创建栈存放中间节点
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node =  stack.pop();
            //根节点入栈
            list.add(node.val);
            //右节点先入栈
            if(node.right != null){
                stack.push(node.right);
            }
            //左节点入栈
            if(node.left != null){
                stack.push(node.left);
            }
        }
        return list;
    }
}

方法2：双层循环

Code：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //非递归算法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        //注意，第一次进入循环的结果是判断根节点root是否为空！
        while(cur != null || !stack.isEmpty()){
            //沿着根的左孩子，依次入栈
            while(cur != null){
                //访问中间结点
                list.add(cur.val);
                stack.push(cur);
                cur = cur.left;
            }
            //直到左孩子为空，说明当前结点的左孩子已经没有了
            //就需要访问当前结点的右孩子
            cur = stack.pop();
            cur = cur.right;
        }
        //返回结果
        return list;
    }
}

3.3 中序遍历（迭代法）

单层循环和双层循环有细微的差别，大家可以自己看代码，根据自己的习惯来写

方法1：单层循环

Code：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        //非递归算法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        //注意，第一次进入循环的结果是判断根节点root是否为空！
        while(cur != null || !stack.isEmpty()){
            //沿着根的左孩子，依次入栈
            if(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            else{
                //直到左孩子为空，说明当前结点的左孩子已经没有了
                //访问中间结点
                cur = stack.pop();
                list.add(cur.val);
                //就需要访问当前结点的右孩子
                cur = cur.right;
            }
        }
        //返回结果
        return list;
    }
}

方法2：双层循环

Code：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        //非递归算法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        //注意，第一次进入循环的结果是判断根节点root是否为空！
        while(cur != null || !stack.isEmpty()){
            //沿着根的左孩子，依次入栈
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            //直到左孩子为空，说明当前结点的左孩子已经没有了
            //访问中间结点
            cur = stack.pop();
            list.add(cur.val);
            //就需要访问当前结点的右孩子
            cur = cur.right;
        }
        //返回结果
        return list;
    }
}

3.4 后序遍历（迭代法）

单层循环和双层循环有细微的差别，大家可以自己看代码，根据自己的习惯来写

方法1：单层循环

这个代码是使用列表反转这个技巧的代码

Code：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        //非递归算法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
            //沿着根的左孩子，依次入栈
            if(cur != null){
                list.add(cur.val);
                stack.push(cur);
                cur = cur.right;
            }
            else{
                //直到左孩子为空，说明已找到可以输出的结点
                cur = stack.pop();
                //判断右孩子
                cur = cur.left;
            }
        }
        //反转
        Collections.reverse(list);
        return list;
    }
}

方法2：双层循环（反转）

这个代码是使用列表反转这个技巧的代码

Code：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        //非递归算法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode cur = root;
        //注意，第一次进入循环的结果是判断根节点root是否为空！
        while(cur != null || !stack.isEmpty()){
            //沿着根的左孩子，依次入栈
            while(cur != null){
                //访问中间结点
                list.add(cur.val);
                stack.push(cur);
                cur = cur.right;
            }
            //直到左孩子为空，说明当前结点的左孩子已经没有了
            //就需要访问当前结点的右孩子
            cur = stack.pop();
            cur = cur.left;
        }
        //反转
        Collections.reverse(list);
        return list;
    }
}

方法3：双层循环（不反转）

这个代码是后序遍历真实的逻辑代码，没有使用反转这个技巧

code：

public List<Integer> postorderTraversal(TreeNode root) {
    //非递归算法
    //1.创建列表返回结果
    List<Integer> ret = new ArrayList<>();
    //2.创建中间过程中间的存放结点的栈
    Stack<TreeNode> stack = new Stack<>();
    //获取当前处理的节点
    TreeNode cur = root;
   	//表示上一个处理的节点
    TreeNode prev = null;
	//3开始进行迭代
    while(cur != null || !stack.empty()) {
        //沿着根的左孩子，依次入栈
        while(cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
		//直到左孩子为空，说明当前结点的左孩子已经没有了
        cur = stack.peek();
        //再来访问右节点，如果右节点没有，就访问并弹出栈顶元素，此时访问的就是中间节点
        //如果有右节点，先判断右节点是否访问过，如果访问过直接弹出
        if(cur.right == null || cur.right == prev) {
            stack.pop();
            ret.add(cur.val);
            prev = cur; // 最近一次访问的节点
        }else{
            cur = cur.right;
        }
    }
    return ret;
}

4.深度优先遍历：统一迭代法

• 利用栈的后入先出特性，按照逆序添加到栈中，然后出栈。同时用一个变量来标记某个节点是否被访问过。栈中的元素是元组，即（节点是否被访问过，节点）

  • 具体来说，当栈不为空时，循环处理最后一个元素：

  • 如果节点为空，则跳过。

  • 如果某个节点没被访问过，则左子节点、右子节点、自己这三个点按照遍历的逆序入栈，并且自己标记为访问过，其他两个子节点标记未访问。

  • 如果某个节点被访问过，则记录它的值。

前序遍历

Code：

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //统一迭代法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Stack<TreeNode> stack = new Stack<>();
        //3.根节点入栈
        if(root != null)
            stack.push(root);
        
        while(!stack.isEmpty()){
            //判断栈顶元素
            TreeNode node = stack.peek();
            if(node != null){
                //为了保证中间结点在左右子树之前先出栈，弹出栈顶元素
                stack.pop();
                //右
                if(node.right != null)
                    stack.push(node.right);
                //左
                if(node.left != null)
                    stack.push(node.left);
                //中
                stack.push(node);
                //并同时给要处理的结点之前添加一个标识
                stack.push(null);
            }
            else {
                //在处理之前弹出栈顶的null
                stack.pop();
                //获取处理的结点
                node = stack.pop();
                //添加中间结点
                list.add(node.val);                
            }
        }
        //返回结果
        return list;
    }
}

中序遍历

Code：

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        //统一迭代法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Stack<TreeNode> stack = new Stack<>();
        //3.根节点入栈
        if(root != null)
            stack.push(root);
        while(!stack.isEmpty()){
            //判断栈顶元素
            TreeNode node = stack.peek();
            if(node != null){
                //为了保证中间结点在左子树之前先出栈，弹出栈顶元素
                stack.pop();
                //右
                if(node.right != null)
                    stack.push(node.right);
                //中
                stack.push(node);
                //并同时给要处理的结点之前添加一个标识
                stack.push(null);
                //左
                if(node.left != null)
                    stack.push(node.left);              
            }
            else {
                //在处理之前天弹出栈顶的null
                stack.pop();
                //获取处理的结点
                node = stack.pop();      
                //添加中间结点
                list.add(node.val);  
            }
        }
        //返回结果
        return list;
    }
}

后序遍历

Code：

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        //统一迭代法
        //1.创建列表返回结果
        List<Integer> list = new ArrayList<>();
        //2.创建中间过程中间的存放结点的栈
        Stack<TreeNode> stack = new Stack<>();
        //3.根节点入栈
        if(root != null)
            stack.push(root);
        while(!stack.isEmpty()){
            //判断栈顶元素
            TreeNode node = stack.peek();
            if(node != null){
                //为了保证中间结点在左子树之前先出栈，弹出栈顶元素
                stack.pop();
                //中
                stack.push(node);
                //并同时给要处理的结点之前添加一个标识
                stack.push(null);
                //右
                if(node.right != null)
                    stack.push(node.right);              
                //左
                if(node.left != null)
                    stack.push(node.left);              
            }
            else {
                //在处理之前天弹出栈顶的null
                stack.pop();
                //获取处理的结点
                node = stack.pop();
                //添加中间结点
                list.add(node.val);              
            }
        }
        //返回结果
        return list;
    }
}

5.广度优先遍历

• 二叉树的广度优先遍历也叫做层序遍历。
• 层序遍历一个二叉树，就是从左到右一层一层的去遍历二叉树。
• 需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

5.1 自顶向下的层序遍历

方法1：递归法

该方法使用的是递归

Code：

class Solution {
    //递归实现
    //1.创建存放结果的列表
    List<List<Integer>> result = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        //2.开始递归
        //递归方法论：
        //明确方法形参和返回值
        levelOrderTraverse(root,0);
        //3.返回结果
        return result;    
    }

    public void levelOrderTraverse(TreeNode node,int depth){
        //判断终止条件
        if(node == null)
            return;
        //确定单层递归逻辑
        depth++;
        if(result.size() < depth){
            //当层增加时，list的Item也增加，利用list的索引值进行层级界定
            List<Integer> list = new ArrayList<>();
            result.add(list);
        }
        result.get(depth - 1).add(node.val);
        levelOrderTraverse(node.left,depth);
        levelOrderTraverse(node.right,depth);
    }
}

方法2：迭代法

该方法使用的迭代法，需要借助队列来实现

Code：

class Solution {
    
    public List<List<Integer>> levelOrder(TreeNode root) {
        //迭代方法
        List<List<Integer>> ret = new ArrayList<List<Integer>>();

        //首先判断特殊情况
        if(root == null){
            return ret;
        } 

        //借助队列实现
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()){
            //创建每一层的列表
            List<Integer> level = new ArrayList<Integer>();
            //获取每一层的元素的个数
            int currentLevelSize = queue.size();
            for(int i = 1;i <= currentLevelSize; ++i){
                TreeNode node = queue.poll();
                level.add(node.val);

                if(node.left != null){
                    queue.offer(node.left);
                }

                if(node.right != null){
                    queue.offer(node.right);
                }

            }
            //将每一层列表添加到结果中
            ret.add(level);
        }
        return ret;
    }
}

5.2 自底向上的层序遍历

方法1：递归法

Code：

class Solution {
    //递归实现
    //1.创建存放结果的列表
    List<List<Integer>> result = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        //2.开始递归
        //递归方法论：
        //明确方法形参和返回值
        levelOrderTraverse(root,0);
        //反转
        Collections.reverse(ret);
        //3.返回结果
        return result;    
    }

    public void levelOrderTraverse(TreeNode node,int depth){
        //判断终止条件
        if(node == null)
            return;
        //确定单层递归逻辑
        depth++;
        if(result.size() < depth){
            //当层增加时，list的Item也增加，利用list的索引值进行层级界定
            List<Integer> list = new ArrayList<>();
            result.add(list);
        }
        result.get(depth - 1).add(node.val);
        levelOrderTraverse(node.left,depth);
        levelOrderTraverse(node.right,depth);
    }
}

方法2：迭代法

Code：

class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        //迭代方法
        List<List<Integer>> ret = new ArrayList<List<Integer>>();

        //首先判断特殊情况
        if(root == null){
            return ret;
        } 

        //借助队列实现
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()){
            //创建每一层的列表
            List<Integer> level = new ArrayList<Integer>();
            //获取每一层的元素的个数
            int currentLevelSize = queue.size();
            for(int i = 0;i < currentLevelSize;i++){
                TreeNode node = queue.poll();
                level.add(node.val);

                if(node.left != null){
                    queue.offer(node.left);
                }

                if(node.right != null){
                    queue.offer(node.right);
                }

            }
            //将每一层列表添加到结果中
            ret.add(level);
            
            //如果不反转就充分利用add函数的性质
            //头插法
            //ret.add(0, level);
        }

        //反转
        Collections.reverse(ret);
        
        return ret;
    }
}

5.3 和层序遍历相关的十一道题目

• 大家做完层序遍历，可以使用层序遍历的方式去做下面的这十一个题目，都与层序bian’li

  • 102.二叉树的层序遍历(opens new window)

  • 107.二叉树的层次遍历II(opens new window)

  • 199.二叉树的右视图(opens new window)

  • 637.二叉树的层平均值(opens new window)

  • 429.N叉树的层序遍历(opens new window)

  • 515.在每个树行中找最大值(opens new window)

  • 116.填充每个节点的下一个右侧节点指针(opens new window)

  • 117.填充每个节点的下一个右侧节点指针II(opens new window)

  • 104.二叉树的最大深度(opens new window)

  • 111.二叉树的最小深度(opens new window)

  • 513.找树左下角的值

参考文献

https://zhuanlan.zhihu.com/p/692543960

https://www.51cto.com/article/614590.html

2

3